Question

In exercises 9 to 12 all solutions to the equations​

Answer 1

The answer to your question are:

9.

a) 11 b) 31

10.

a) 1/5 b) do not exist

11.

a) √11 b) √8

12

a) ∛-3 b) ∛4

Explanation:

9a

f(x) = x² - 5

f(4) = (4)² - 5 = 16 - 5 = 11

9b

f(-6) = (-6)² - 5 = 36 - 5 = 31

10 a

f(x ) = -1/x

f(-5 ) = -1/x = -1/-5 = 1/5

f(0 ) = -1/0 do not exist

11a

f(x) = √(x + 7)

f(4) = √(4 + 7)

f(x) = √11

b) f(1) = √(1 + 7)

f(1) = √8

12a

f(x) = ∛ (x - 1)

f(-2) = ∛ (-2 - 1)

f(-2) = ∛ -3

b)

f(3) = ∛ (3 - 1)

f(3) = ∛ 4

Answer 2

12b. 28 = x

12a. -7 = x

11b. -6 = x

11a. 9 = x

10b. UNDEFINED

10a. -⅕ = x

9b. i = x

9a. ±3 = x

Explanation:

12. Cube both sides of both equations, then solve for x:

`12b. \: 3 = \sqrt[3]{x - 1} >> 27 = x - 1 \\ \\ 28 = x \\ \\ 12a. \: -2 = \sqrt[3]{x - 1} >> -8 = x - 1 \\ \\ -7 = x`

11. Square both sides of both equations, then solve for x:

`11b. \: 1 = √(x + 7) >> 1 = x + 7 \\ \\ -6 = x \\ \\ 11a. \: 4 = √(x + 7) >> 16 = x + 7 \\ \\ 9 = x`

10. Dividing is the same as multiplying by the multiplicative inverse of another term:

`10a. \: -5 = (1)/(x) >> -5 = {x}^( -1) \\ \\ -(1)/(5) = x`

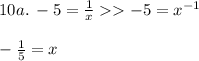
* ⁻¹ indicates the multiplicative inverse of -⅕, which is -5. Then there is 1⁄0, which is undefined.

9.

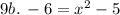
`9b. \: -6 = {x}^(2) - 5`

+ 5 + 5

____________________

-1 = x²

`i = x`

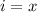
According to the Complex Number System, the iota symbol can be either complex or real:

`√(-1) = i \\ -1 = {i}^(2) \\ -i = {i}^(3) \\ 1 = {i}^(4)`

I am joyous to assist you anytime.