Question

Block with m = 300 grams oscillates at the end of a linear spring with k = 6.5 N/m. (assume this is a top-down view and the block is sliding on a frinctionless surface; neglect gravity)

a) what is the period of the block's motion in seconds

b) if the blovk's max acceleration is 2 m/s^2, what is the amplitude of the motion (m)

Answer 1

Step-by-step explanation:

Given that,

Mass of the block, m = 300 g = 0.3 kg

Linear spring constant, k = 6.5 N/m

(a) Let T is the period of the block's motion. It is given by :

`T=(2\pi)/(\omega)`

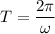
where

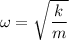`\omega=\sqrt{(k)/(m)}`= angular frequency

Also,
`\omega=\sqrt{(k)/(m)}`

`T=\frac{2\pi}{\sqrt{(k)/(m)}}`

`T=\frac{2\pi}{\sqrt{(6.5)/(0.3)}}`

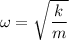
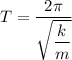
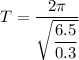
T = 1.34 seconds

(b) The maximum acceleration of the block is,
`a_(max)=2\ m/s^2`

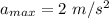
The maximum acceleration is given by :

`a_(max)=\omega^2A`

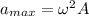
A is the amplitude of the motion,

`A=(a_(max))/(\omega^2)`

`A=\frac{a_(max)}{(\sqrt{(k)/(m)})^2}`

`A=(ma_(max))/(k)`

`A=(0.3* 2)/(6.5)`

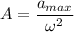
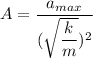
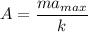
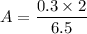
A = 0.09 meters

Hence, this is the required solution.