Question

- If an unbiased coin is tossed four times, are the following the events A and B conditionally independent given C : A={There is at least one Tail in the first 3 tosses} B ={There is at least one Head in the last 3 tosses} C = {The second and third toss respectively reveal Heads, Tails}

Answer 1

A and C are not independent.

B and C are not independent either.

Explanation:

By the multiplication rule, the sampling space has
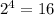`2^4=16` possible outcomes.

Let's compute P(A), P(B), P(C), P(A∩C), P(B∩C), P(A|C) and P(B|C).

As there are only two outcomes that does not have at least on tail in the first three tosses (H,H,H,H) and (H,H,H,T) then

P(A) = 14/16 = 7/8

Similarly, as there are only two outcomes that does not have at least on head in the last three tosses (H,T,T,T) and (T,T,T,T) then

P(A) = 14/16 = 7/8

A∩C and B∩C have 4 possible outcomes (T,H,T,T), (T,H,T,H), (H,H,T,T) and (H,H,T,H), so

P(A∩C) = P(B∩C) = 4/16 = ¼

P(A) given C and P(B) given C have the following probabilities:

`P(A|C)=(P(A\cap C))/(P(C))=(1/4)/(1/4)=1`

`P(B|C)=(P(B\cap C))/(P(C))=(1/4)/(1/4)=1`

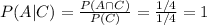
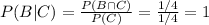
Since P(A|C)≠P(A), A and C are not independent

Since P(B|C)≠P(B), B and C are not independent