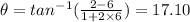What is the equation of the line that passes through (6, 1) and is perpendicular to the line y 3x+2? CI) At what angle do the lines y= 6x +4 and y-2x+3 cross?

Question

asked Aug 8, 2020 80.0k views

1 Answer

Mchouhan · Answer 1 · 2020-08-12T16:44:29+0000

Answer with explanation:

The equation of any line with slope 'm' and passing through any point
(x_1,y_1) is given by

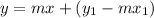
y=mx+(y_1-mx_1)

As we know that the general equation of a line with slope 'm' is
y=mx+c

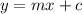
Comparing with the given equation
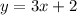y=3x+2 we can conclude slope of the given line is
m_1=3

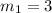
Now we know that the product of slopes of perpendicular lines is -1

Mathematically we can write for perpendicular lines

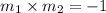
m_1* m_2=-1

Thus the slope of the required line is obtained from the above relation since it is given that they are perpendicular

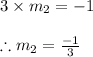
$3* m_(2)=-1\\\\\therefore m_(2)=(-1)/(3)$

Hence using the given and the obtained values the equation of the required line is

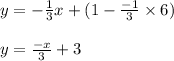
$y=-(1)/(3)x+(1-(-1)/(3)* 6)}\\\\y=(-x)/(3)+3$

Part b)

The angle of intersection between 2 lines with slopes
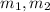m_(1),m_2 is given by

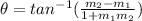
$\theta =tan^(-1)((m_2-m_1)/(1+m_1m_2))$

Comparing the equations of given lines

$y=6x+3\\\\y=2x+3$

with the standard equation we get

$m_(1)=6\\\\m_(2)=2$

Thus the angle of intersection becomes

$\theta =tan^(-1)((2-6)/(1+2*6))=17.10$