Question

a) Give the definition of sequence of real numbers (Xn). Then give 2 example. b) Give the definition of convergent sequence. Then give 2 example. c) Give the definition of Cauchy sequence. Then give an example 0. d) Show that lim n+1 72

Answer 1

a) Definition of sequence of real numbers: A sequence of real number is the function from set of natural number to the set of real numbers. i.e.

f: N → R

Example:
`S_(n)=(1)/(n)`

`S_(n)=(n)/(n+1)`

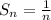
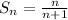
b) Definition of convergent sequence: A sequence is said to be convergent if for very large value of n, function will give the finite value.

Example:
`S_(n)=(1)/(n)`

`S_(n)=(n)/(n+1)`

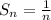
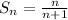
c) Definition of Cauchy sequence: A sequence is said to be Cauchy Sequence if terms of sequence get arbitrary close to one another.