Answer:
55.4 hours
Explanation:
Let A = First pump
B = Second pump
C = Third pump
From the given informations,
we know that A takes 60 hours to fill a reservoir.
Thus, it can be written as
% done by A in 60 hours = 100% = 1
60 (% done by A in 1 hour) = 1
% done by A in 1 hour = 1/60
Similarly,
% done by B in 1 hour = 1/80
% done by C in 1 hour =-(1/90)
Note: negative value because pump c is used to empty the reservoir.
Now we have formed three equations,
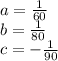
We want to find how long it takes to fill up the reservoir when three of them work together.
Thus,

where t is the time taken
a = % done by A in 1 hour
b = % done by B in 1 hour
c = % done by C in 1 hour
To find the value of t, just adds up the three equations formed previously.
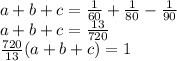
Thus, t = 720/13 = 55.4 hours