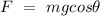Question

A wheel initially spinning at wo = 50.0 rad/s comes to a halt in 20.0 seconds. Determine the constant angular acceleration and the number of revolutions it makes before stopping. An athlete is holding a 2.5 meter pole by one end. The pole makes an angle of 60 with the horizontal. The mass of the pole is 4 kg. Determine the torque exerted by the pole on the athlete's hand. (The mass of the pole can be assumed to be concentrated at the center of mass.)

Answer 1

part (a)
`\alpha\ =\ -2.5\ rad/s^2`

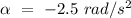
part (b) N = 79.61 rev

part (c)
`\tau\ =\ 23.54\ Nm`

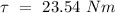
Step-by-step explanation:

Given,

• Initial speed of the wheel =
  `w_o\ =\ 50.0\ rad/s`
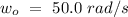
• total time taken = t = 20.0 sec

part (a)

Let
`\alpha` be the angular acceleration of the wheel.

Wheel is finally at the rest. Hence the final angular speed of the wheel is 0.

`\therefore w_f\ =\ w_0\ +\ \alpha t\\\Rightarrow \alpha\ =\ -(w_0)/(t)\\\Rightarrow \alpha\ =\ -(50)/(20)\\\Rightarrow \alpha\ =\ -2.5\ rad/s^2`

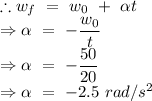
part (b)

Let
`\theta` be the total angular displacement of the wheel from initial position till the rest.

`\therefore \theta\ =\ w_0t\ +\ (1)/(2)\alphat^2\\\Rightarrow \theta\ =\ 50* 20\ -\ 0.5* 2.5* 20^2\\\Rightarrow \theta\ =\ 500\ rad`

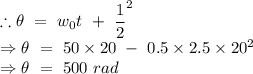
We know, 1 revolution =
`2\pi` rad

Let N be the number of revolution covered by the wheel.

`\therefore N\ =\ (\theta)/(2\pi)\\\Rightarrow N\ =\ (500)/(2* 3.14)\\\Rightarrow N\ =\ 79.61\ rev`

Hence the 79.61 revolution is covered by the wheel in the 20 sec.

part (c)

Given,

• Mass of the pole = m = 4 kg
• Length of the pole = L = 2.5 m
• Angle of the pole with the horizontal axis =
  `\theta\ =\ 60^o`

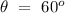
Now the center of mass of the pole =
`d\ =\ \dfra{L}{2}\ =\ (2.5)/(2)\ =\ 1.25\ m`

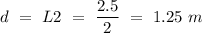
Weight component of the pole perpendicular to the center of mass =
`F\ =\ mgcos\theta`

`\therefore \tau\ =\ F* d\\\Rightarrow \tau\ =\ 4* 9.81* cos60^o* 1.25\\\Rightarrow \tau\ =\ 23.54\ Nm`