Question

Avoiding an accident while driving can depend on reaction time. Suppose that reaction time, measured from the time the driver first sees the danger until the driver gets his/her foot on the brake pedal, is approximately symmetric and mound-shaped with mean 1.7 seconds and standard deviation 0.12 seconds. Use the 68-95-99.7 rule to answer the following questions. This web site 68-95-99.7 rule graphically depicts the 68-95-99.7 rule and may help with the following questions. What percentage of drivers have a reaction time more than 1.94 seconds? % What percentage of drivers have a reaction time less than 1.58 seconds? % What percentage of drivers have a reaction time less than 1.82 seconds? %

Answer 1

2.5% of the drivers have a reaction time of more than 1.94 seconds.

16% of the drivers have a reaction time of less than 1.58 seconds

84% of the drivers have a reaction time of less than 1.82 seconds.

Explanation:

The 68-95-99.7 rule states that, when X is an observation from a random moundshaped (normally distributed) value with mean
`\mu` and standard deviation
`\sigma`, we have these following probabilities:

There is a 68% probability that X is within 1 standard deviation of the mean(34% probability that is above, 34% probability that is below).

There is a 95% probability that X is within 2 standard deviations of the mean(47.5% above, 47.5% below)

There is a 99.7% probability that X is within 3 standard deviations of the mean(49.85% above, 49.85% below).

In our problem, we have that:

The mean is
`\mu = 1.7`

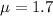
The standard deviation is
`\sigma = 0.12`

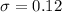
What percentage of drivers have a reaction time more than 1.94 seconds?

1.94 is two standard deviations above the mean.

There is a 50% probability that X is below the mean and 50% above. If it is above, there is 95% probability that the driver has a reaction time within 2 standard deviations of the mean, this means a reaction time of LESS THAN 1.94 seconds.

So the probability that he has a reaciton time of more than 1.94 seconds is:

`P = 1 - (0.50 + 0.50*(0.95)) = 0.025`

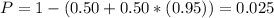
2.5% of the drivers have a reaction time of more than 1.94 seconds.

What percentage of drivers have a reaction time less than 1.58 seconds?

1.58 seconds is one standard deviation below the mean

Of those 50% who are below the mean, 68% are within one standard deviation of the mean. This means that 32% percent of those are below one standard deviation of the mean. So

`P = 0.5*0.32 = 0.16`

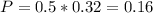
16% of the drivers have a reaction time of less than 1.58 seconds

What percentage of drivers have a reaction time less than 1.82 seconds?

1.58 seconds is one standard deviation above the mean

50% of the drivers are below the mean. So 50% already have a reaction time of less than 1.82 seconds.

Of the 50% that are above the mean, 68% are within one standard deviation. So

`P = 0.5 + 0.5(0.68) = 0.84`

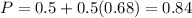
84% of the drivers have a reaction time of less than 1.82 seconds.