Answer:
a) There is a 7.14% p(a) probability that a randomly chosen adult who is obese also suffers from diabetes.
b) There is a 66.64% probability of the adult being obese, given that he suffers from diabetes.
Step-by-step explanation:
The problem states that:
28% of all adults are obese. This means that there is a 28% probability of a randomly chosen adult being obese.
3% of all adults suffer from diabetes. This means that there is a 3% probability of a randomly chosen adult suffering from diabetes.
2% of all adults both are obese and suffer from diabetes. This means that there is a 2% probability of a randomly chosen adult both being obese and suffering from diabeters.
(a) Find the probability that a randomly chosen adult who is obese also suffers from diabetes. Round your answer to decimal places:
28% of all adults are obese and 2% of all adults are both obese and suffer from diabetes.
So the probability of a randomly chosen adult who is obese suffering from diabetes is:
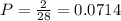
There is a 7.14% probability that a randomly chosen adult who is obese also suffers from diabetes.
(b) Find the probability that a randomly chosen adult is obese, given that he or she suffers from diabetes.
What is the probability of B happening, knowing that A has happened.
It can be calculated by the following formula
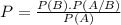
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.
So:
What is the probability of the adult being obese, given that he suffers from diabetes.
P(B) is the probability of the adult being obese. So
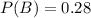
P(A/B) is the probability of the adult suffering from diabetes, given that he is obese. We found in a) that 7.14% of the adults who are obese also suffer from diabetes. So:
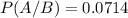
P(A) is the probability of the adult suffering from diabetes. So:
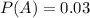
Finally
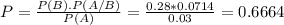
There is a 66.64% probability of the adult being obese, given that he suffers from diabetes.