Question

Calculate the The wavelength of the first Balmer series of hydrogen is 6562 following: a) The ionization potential, and b) The first excitation potential of the hydrogen atom.

Answer 1

(a) 13.6 eV

(b) 10.2 V

Step-by-step explanation:

a) Ionization potential energy is the least requirement of energy to fetch a neutral atom from its initial state to its ionized state i.e basically the minimum energy required to excite an electron from n=1 to infinity.

Energy of a level, n, in Hydrogen atom is,
`E_(n)=-(13.6)/(n^(2) )`

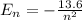
Now ionization potential can be calculated as

`E_(\infty ) -E_(1 )`

Substitute all the value of energy and n in above equation.

`=-(13.6)/(\infty^(2) )--(13.6)/(1^(2))\\=13.6 eV`

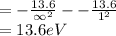
Therefore, the ionization potential is 13.6 eV.

b) This is the energy required to excite a atom from ground state to its excited state. When electrons jumps from ground state level(n=1) to 1st excited state(n=2) the corresponding energy is called 1st excitation potential energy and corresponding potential is called 1st excitation potential.

So, 1st excitation energy = E(n 2)- E(n = 1)

So,

`=-(13.6)/(2^(2) )--(13.6)/(1^(2))\\=-3.4eV-(-13.6eV)\\=10.2eV`

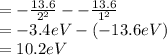
Now we can find that 1st excitation energy is 10.2 eV which gives,

`eV'=10.2eV\\V'=10.2V`

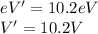
Therefore, the 1st excitation potential is 10.2V.