Question

Starting from rest, an elevator accelerates uniformly between the 1st and 2nd floors, and decelerates uniformly between the 5th and 6th floors, coming to a stop at the 6th floor. In between, the elevator covers the 6 meter distance between two adjacent floors in 1 s. Inside, Liz (who is about to graduate), is standing on a scale that reads 800 N when the elevator isn't moving. What was her minimum scale reading during the trip? (Use g = 10 m/s2)

Answer 1

The minimum scale reading during the trip was 560N.

Step-by-step explanation:

So, in order to solve this problem, we must first prepare a drawing that will represent the situation. (See picture attached)

In the drawing we have the three situations represented. When the elevator goes up, when it travels at a constant velocity and when it decelerates.

We can now do an analysis of each of the situations:

When elevator starts moving:

When the elevator starts moving, it will be accelerated upwards, so the sum of forces will be equal to the mass times the acceleration. In this case, we have two forces, Weight and the normal force, which is the force the floor of the elevator is making upon the scale. This is the reading the scale will give you.

ΣF=ma

-W+N=ma

N=ma+W

As you may see, in this case the weight is added to the force applied by the elevator to accelerate, so the scale reading will be maximum here.

When the elevator has constant velocity:

If the elevator has constant velocity, then its acceleration will be zero, so the sum of the forces will be equal to zero.

ΣF=0

-W+N=0

N=W

On this stage, the scale will return a reading of 800N, since it will not be accelerated.

When the elevator is decelerating:

On the final stage of the trip, the elevator will have a negative acceleration (it is decelerating) so the sum of the forces will be equal to the product between the mass and the acceleration, so we get:

ΣF=-ma

-W+N=-ma

N=W-ma

In this final stage, we can see that the elevator's force is being subtracted from the weight due to the loss of velocity. This is where the scale will give you a minimum reading, so we analyze this stage.

Weight is found by multiplying mass and the acceleration of gravity:

W=mg

so we can rewrite our equation as:

N=mg-ma

when factoring the mass we get:

N=m(g-a)

the mass can be found by dividing the weight into the acceleration of gravity:

W=mg

`m=(W)/(g)`

`m=(800N)/(10(m)/(s^(2)))`

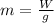
m=80kg

we know that in the middle of the trip, the elevator will travel 6m in 1s, so the constant velocity is:

`V=(d)/(t)`

`V=(6m)/(1s)`

`V=6(m)/(s)`

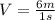
this is the initial velocity for the final stage. The acceleration of the final stage can be found with the following formula:

`a=(V_(f)^(2)-V_(0)^(2))/(2x)`

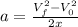
the final velocity is zero since it goes to a stop, so the formula becomes:

`a=(-V_(0)^(2))/(2x)`

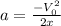
when substituting we get:

`a=(-(6m/s)^(2))/(2(6m))`

`a=-3(m)/(s^(2))`

When substituting values we can now find the scale's reading:

`N=80kg(10m/s^(2)-3m/s^(2))`

`N=80kg(7m/s^(2))`

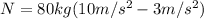
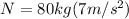
N=560N

So the minimum scale reading during the trip was 560N