Salary relationships usually have behaviors that can be expressed through mathematical equations, for this case we must locate the information they give us, according to which the salary of the movie star
 is equal to a fixed basic remuneration
is equal to a fixed basic remuneration
 plus a percentage
plus a percentage
 of the gross income
of the gross income
 , that is:
, that is:

With this equation and the data they give us, we can solve the request so :
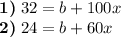
We clear the basic remuneration
 from the second equation and replace in the first:
from the second equation and replace in the first:
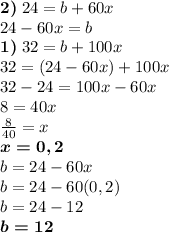
Thus, with the fixed basic remuneration and the percentage of gross income calculated, we can estimate how much the following film should obtain so that the movie star obtains at least
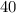 millions salary:
millions salary:
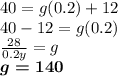
Answer
The minimum amount of gross income that the next film should generate is
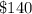 millions
millions