Question

On a given week, the classical literature section in a certain library had 40 different books, all of which were in stock on the shelf on Monday morning. If 50 percent of the books that were borrowed during the week were returned to the library on or before Saturday morning of that same week, and if there were at least 22 books on the shelf that Saturday morning, what is the greatest number of the books that could have been borrowed during the week?

Answer 1

The greatest number of the books that could have been borrowed during the week are 36.

Explanation:

Let the total number of books or N = 40

Let the number of borrowed books be = B

As given, the number of books available are greater than 22.

We get the following equation as per scenario:

`(B)/(2)+(N-B) \geq 22`

=>
`B+2N-2B \geq 44`

=>
`2N-B \geq 44`

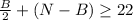
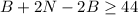
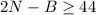
Substituting N = 40, we get ;

`B\leq 36`

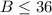
Therefore, the maximum possible number of borrowed books will be 36.

Answer 2

The greatest number of the books that could have been borrowed during the week is 36

Explanation:

Let's create an equation which represent this problem, where will rest the book borrow and add the book returned to the 40 initial amount of book on Monday, to get the 22 book in the shelf on Saturday morning

40 (book on the shelf on Monday) - x (book borrowed) + 0.5 * x (50 % of the book was returned before Saturday) = 22 (books in the shelf on Saturday morning)

40 - x + 0.5 * x = 22

40 - 0.5*x = 22

18 = 0.5 * x

18/0.5 = x

36 = x

The amount of borrowed books is 36