Question

In the right △ABC m∠C=90°,

BL
is an angle bisector of ∠ABC. What is the ratio CL:AC, if m∠BAC=30°?
CL : AC =

Answer 1

1/3

Explanation:

here is use without tangent and cos with proof:

Answer 2

`(CL)/(AC)=(1)/(3)`

Explanation:

see the attached figure to better understand the problem

we know that

m∠BAC+m∠ABC=90° -----> by complementary angles

m∠BAC=30° ----> given problem

so

m∠ABC=60°

If BL is an angle bisector of m∠ABC

then

m∠ABL=m∠LBC=30°

In the right triangle LBC

`tan(30\°)=CL/BC`

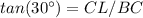
Solve for BC

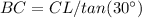`BC=CL/tan(30\°)` ----> equation A

In the right triangle ABC

`tan(60\°)=AC/BC`

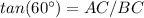
Solve for BC

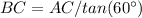`BC=AC/tan(60\°)` ----> equation B

Equate equation A and equation B

`(CL)/(tan(30\°))=(AC)/(tan(60\°))`

`(CL)/(AC)=(tan(30\°))/(tan(60\°))`

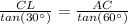
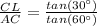
Remember that

`tan(30\°)=(√(3))/(3)`

`tan(60\°)=√(3)`

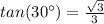
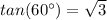
substitute

`(CL)/(AC)=(1)/(3)`