Question

As part of calculations to solve an oblique plane triangle (ABC), the following data was available: b=50.071 horizontal distance, C=90.286° (decimal degrees), B=62.253° (decimal degrees). Calculate the distance of c to 3 decimal places (no alpha).

Answer 1

The distance of c is 56.57.

Step-by-step explanation:

Given that,

Horizontal distance b = 50.071

Angle B =62.253°

Angle C= 90.286°

We need to calculate the distance of c

Using sine law

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

`(b)/(\sin B)=(c)/(\sin C)`

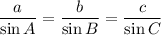
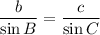
Put the value in to the formula

`(50.071)/(\sin62.253)=(c)/(\sin90.286)`

`c=(50.071)/(\sin62.253)*\sin90.286`

`c=56.57`

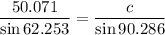
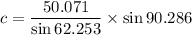
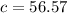
Hence, The distance of c is 56.57.