Answer:
ht = 776.63 km above earth's surface
Step-by-step explanation:
Since the satellite is moving in a circular path, we know that:
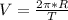 Let this be eq1
Let this be eq1
If now we express the sum of forces on the satellite:
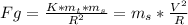 Replacing the value from eq1 into this equation:
Replacing the value from eq1 into this equation:
 Solving for R:
Solving for R:
![R = \sqrt[3]{(K*m_t*T^2)/((2\pi )^2) } =7.15*10^6m](https://img.qammunity.org/2020/formulas/physics/college/cft6lucjkv68p7e276rgmvwpfpi8v7m3ov.png) If we subract the earth radius from this value, we'll get the altitude above earth's surface:
If we subract the earth radius from this value, we'll get the altitude above earth's surface:
ht = 776.63 km