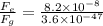Question

In a Hydrogen atom an electron rotates around a stationary proton in a circular orbit with an approximate radius of r =0.053nm. (a) Find the magnitude of the electrostatic force of attraction, Fe between the electron and the proton. (b) Find the magnitude of the gravitational force of attraction Fg , between the electron and the proton, and find the ratio, Fe /Fg . me = 9.11 x 10-31kg, e = 1.602 x 10-19C mp = 1.67 x 10-27kg k = 9 x 109 Nm2 /C2 G = 6.67 x 10-11 Nm2 /kg2

Answer 1

(a) 8.2 x 10^-8 N

(b) 3.6 x 10^-47 N , 2.27 x 10^39

Step-by-step explanation:

charge of proton, q1 = 1.6 x 10^-19 C

charge of electron, q2 = - 1.6 x 10^-19 C

radius of orbit, r = 0.053 nm = 0.053 x 10^-9 m

mass of electron, me = 9.1 x 10^-31 kg

mass of proton, mp = 1.67 x 10^-27 kg

Gravitational constant, G = 6.67 x 10^-11 Nm^2/kg^2

(a) The electrostatic force between two charges is given by

`F_(e)=(Kq_(1)q_(2))/(r^2)`

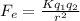
Where, K is the coulombic constant = 9 x 10^9 Nm^2/C^2

By substituting the values

`F_(e)=(9* 10^(9)* 1.6* 10^(-19)\1.6* 10^(-19))/(\left ( 0.053 * 10^(-9) \right )^2)`

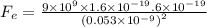
Fe = 8.2 x 10^-8 N

(b) The gravitational force between the electron and proton is given by

`F_(g)=(Gm_(e)m_(p))/(r^(2))`

`F_(g)=(6.67* 10^(-11)* 9.1* 10^(-31)\1.67* 10^(-27))/(\left ( 0.053 * 10^(-9) \right )^2)`

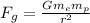
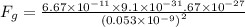
Fg = 3.6 x 10^-47 N

`(F_(e))/(F_(g))=(8.2*10^(-8))/(3.6* 10^(-47))`

`(F_(e))/(F_(g))=2.27* 10^(39)`