Question

Two 1.1 kg masses are 1 m apart (center to center) on a frictionless table. Each has +10 JC of charge. What is the initial acceleration (in m/s2) of this massif it is released and allowed to move?

Answer 1

The initial acceleration of the mass, if it is released and allowed to move =
`0.8182\ m/s^2.`

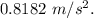
Step-by-step explanation:

Given:

• Mass of each object,
  `\rm m = 1.1\ kg.`
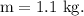
• Charge on each object,
  `\rm q = +10\ \mu C=+10* 10^(-6)\ C.`
• Distance between the objects,
  `\rm r=1\ m.`

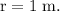
There are two forces that will act on these objects:

1. Gravitational force due to masses of the objects, which is attractive.
2. Electrostatic force due to the charges on the objects, which is repulsive because both the objects have positive charges.

The gravitational force between two masses
`\rm m_1` and
`\rm m_2`, separated by distance
`\rm r` is given by

`\rm F_g = (Gm_1m_2)/(r^2).`

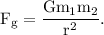
where,

G is the Universal Gravitational constant, having value =
`\rm 6.67* 10^(-11)\ m^3kg^(-1)s^(-2).`

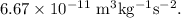
Therefore, the gravitational force between these masses is

`\rm F_g=(Gmm)/(r^2)\\=((6.67* 10^(-11))* (1.1)* (1.1))/(1^2)\\=8.0707* 10^(-11)\ N.`

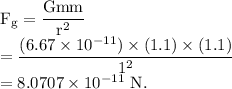
The electrostatic force between two charges
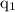`\rm q_1` and
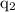`\rm q_2`, separated by distance
`\rm r` is given by

`\rm F_e = (kq_1q_2)/(r^2).`

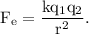
where,

k is the Coulomb's constant, having value =
`\rm 9* 10^(9)\ C^2N^(-1)m^(-2).`

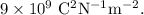
Therefore, the electrostatic force between these masses is

`\rm F_e=(kqq)/(r^2)\\=((9* 10^(9))* (10* 10^(-6))* (10* 10^(-6)))/(1^2)\\=0.9\ N.`

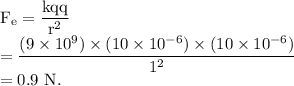
Since, one force is attractive and another is repulsive, therefore, the net force that one mass exerts on another is given by

`\rm F=F_e-F_g\\=0.90-8.0707* 10^(-11)\\=0.90\ N.`

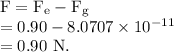
According to Newton's second law of motion,

`\rm F=ma\\\\a\ is\ the\ acceleration\ of\ the\ mass.\\\rm\\\Rightarrow a = \frac Fm=(0.90)/(1.1)=0.8182\ m/s^2.`

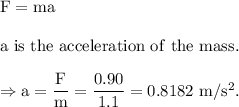
It is the acceleration with which the mass starts to move.