Answer:
1.V= 640.48 m/s :total velocity in t= 5s
2. Y= 5.79m : vertical distance above the height of release (in meters) where the ball will hit a wall 13.0 m away
3. v =25m/s
4. s= (-1.5t³+26t ) m
Step-by-step explanation:
1. Parabolic movement in the x-y plane , t=5s
V₀=638.6 m/s=Vx :Constant velocity in x
Vy=V₀y +gt= 0+9.8*5 = 49 m/s : variable velocity in y
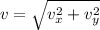
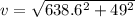
V= 640.48 m/s : total velocity in t= 5s
2.
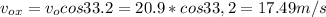
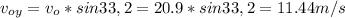
x=v₀x*t
13=v₀x*t
13=17.49*t
t=13/17.49=0.743s : time for 13.0 m away
th=v₀y/g=11.44/9.8= 1,17s :time for maximum height
at t=0.743 sthe ball is going up ,then g is negative
y=v₀y*t - 1/2 *g¨*t²
y=11.44*0.743 -1/2*9.8*0.743²
y= 5.79m : vertical distance above the height of release (in meters) where the ball will hit a wall 13.0 m away
3. s = (1t3 + -5t2 + 3) m
v=3t²-10t=3*25-50=75-50=25m/s
at t=0, s=3 m
at t=5s s=5³-5*5²+3
4. a = (-9t) m/s2
a=dv/dt=-9t
dv=-9tdt
v=∫ -9tdt
v=-9t²/2 + C1 equation (1)
in t=0 , v₀=26m/s ,in the equation (1) C1= 26
v=-9t²/2 + 26=ds/dt
ds=( -9t²/2 + 26)dt
s= ∫( -9t²/2 + 26)dt
s= -9t³/6+26t+C2 Equation 2
t = 0, s = 0 , C2=0
s= (-9t³/6+26t ) m
s= (-1.5t³+26t ) m