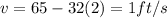Answer:
a)
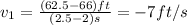
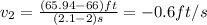
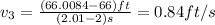

b)
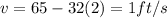
Step-by-step explanation:
From the exercise we got the ball's equation of position:
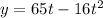
a) To find the average velocity at the given time we need to use the following formula:

Being said that, we need to find the ball's position at t=2, t=2.5, t=2.1, t=2.01, t=2.001
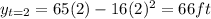
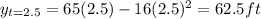
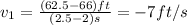
--
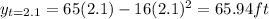
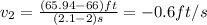
--
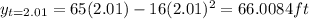
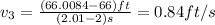
--
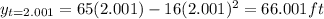

b) To find the instantaneous velocity we need to derivate the equation