Question

What are the (time varying) amplitudes of the E and H fields if summer sunlight has an intensity of 1150 W/m2 in any Town?

Calculate the relative strength of the gravitational and solar electromagnetic pressure forces of the sun on the earth.

Answer 1

Step-by-step explanation:

Given that,

Intensity = 1150 W/m²

(a). We need to calculate the magnetic field

Using formula of intensity

`I=(E^2)/(2\mu_(0)c)`

`E=\sqrt{2* I\mu_(0)c}`

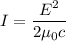
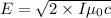
Put the value into the formula

`E=\sqrt{2*1150*4\pi*10^(-7)*3*10^(8)}`

`E=931.17\ N/C`

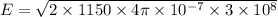
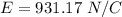
Using formula of magnetic field

`B = (E)/(c)`

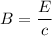
Put the value into the formula

`B=(931.17)/(3*10^(8))`

`B=0.0000031039\ T`

`B=3.10*10^(-6)\ T`

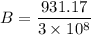
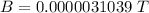
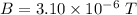
(b). The relative strength of the gravitational and solar electromagnetic pressure forces of the sun on the earth

We need to calculate the gravitational force

Using gravitational force

`F=(Gm_(s)M_(e))/(r^2)`

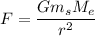
Put the value into the formula

`F=(6.67*10^(-11)*1.98*10^(30)*5.97*10^(24))/((1.496*10^(11))^2)`

`F=3.522*10^(22)\ N`

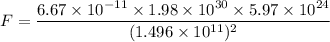
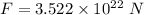
We need to calculate the radiation force

Using formula of force

`F_(R)=(I)/(c)\pi*R_(E)^(2)`

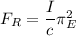
Put the value into the formula

`F_(R)=(1150)/(3*10^(8))*\pi*(6.378*10^(6))^2`

`F_(R)=4.8*10^(8)\ N`

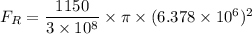
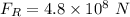
The gravitational and solar electromagnetic pressure forces of the sun on the earth

`(F_(G))/(F_(R))=(3.522*10^(22))/(4.8*10^(8))`

`(F_(G))/(F_(R))=7.3375*10^(13)`

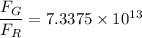
Hence, This is the required solution.