Answer:
The possible thickness of the soap bubble =
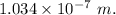
Step-by-step explanation:
Given:
- Refractive index of the soap bubble,
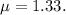
- Wavelength of the light taken,
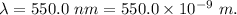
Let the thickness of the soap bubble be
 .
.
It is given that the soap bubble appears very bright, it means, there is a constructive interference takes place.
For the constructive interference of light through a thin film ( soap bubble), the condition of constructive interference is given as:
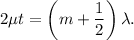
where
 is the order of constructive interference.
is the order of constructive interference.
Since the soap bubble is appearing very bright, the order should be 0, as
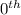 order interference has maximum intensity.
order interference has maximum intensity.
Thus,
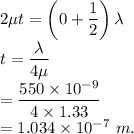
It is the possible thickness of the soap bubble.