Answer:
The electric flux is
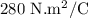
Step-by-step explanation:
Given:
- Radius of the disc R=0.50 m
- Angle made by disk with the horizontal
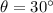
- Magnitude of the electric Field
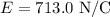
The flux of the Electric Field E due to the are dA in space can be found out by using Gauss Law which is as follows
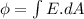
where
 is the total Electric Flux
is the total Electric Flux- E is the Electric Field
- dA is the Area through which the electric flux is to be calculated.
Now according to question we have
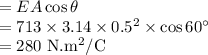
Hence the electric flux is calculated.