Question

A 20-lb force acts to the west while an 80-lb force acts 45° east of north. The magnitu 80 lb 70 lb 067 lb 100 lb

Answer 1

• The magnitude of the resulting force is 67 lbf.

Step-by-step explanation:

Taking the east as the positive x direction, and the north as the positive y direction.

The first force points west, this is, in the direction of
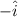`-\hat{i}`, so, is

`\vec{F}_1 = - 20 \ lbf \ \hat{j}`

`\vec{F}_1 = (0 , - 20 \ lbf \)`

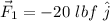
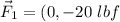
For the second force, knowing the magnitude and directions relative to the x axis, we can find Cartesian representation of the vectors using the formula

`\ \vec{A} = | \vec{A} | \ ( \ cos(\theta) \ , \ sin (\theta) \ )`

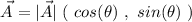
where
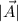`| \vec{A} |` is the magnitude of the vector and θ the angle with the positive x direction.

So, the second force is

`\vec{F}_2 = 80 \ lbf \ \ ( \ cos(45 \°) \ , \ sin (45 \°) \ )`

`\vec{F}_2 = ( \ 56.5685 \ lbf \ , \ 56.5685 \ lbf \ )`

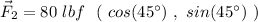
The net force will be :

`\vec{F}_(net) = \vec{F}_1 + \vec{F}_2`

`\vec{F}_(net) = (0 , - 20 \ lbf \) + ( \ 56.5685 \ lbf \ , \ 56.5685 \ lbf \ )`

`\vec{F}_(net) =  ( \ 56.5685 \ lbf \ , \ 56.5685 \ lbf \ - 20 \ lbf  )`

`\vec{F}_(net) =  ( \ 56.5685 \ lbf \ , \ 36.5685 \ lbf \  )`

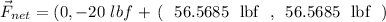
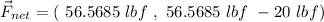
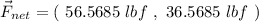
To obtain the magnitude, we can use the Pythagorean Theorem

`|\vec{F}_(net)| = \sqrt{F_(net_x)^2 +F_(net_y)^2}`

`|\vec{F}_(net)| = √(( \ 56.5685 \ lbf \ )^2 +( \ 36.5685 \ lbf \ )^2)`

`|\vec{F}_(net)| = 67.36 \ lbf`

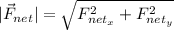
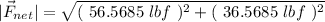
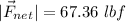
And this is the magnitude we are looking for.