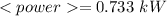What power in Kw is required to transfer a charge of 9000 coulomb through a potential difference of 220 volts in 45 min? 0.9 kW 0.73 kW 0.5 kW 1.6 kW

Question

asked May 26, 2020 20.4k views

1 Answer

Milad Ahmadi · Answer 1 · 2020-05-30T01:51:07+0000

Answer:

Step-by-step explanation:

The work W required for the transfer is equal to the energy difference

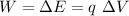
$W = \Delta E = q \ \Delta V$

where q is the charge we want to transfer and ΔV is the potential difference.

So, the work needed will be

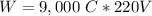
$W = 9,000 \ C * 220 V$

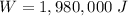
$W = 1,980,000 \ J$

Now, the average power is:

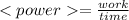
< power > = (work)/(time)

As the Watt is Joule/second, we need the 45 min multiplied by 60:

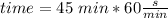
$time = 45 \ min * 60 (s)/(min)$

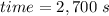
$time = 2,700 \ s$

Taking all this together:

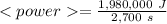
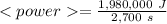
$< power > = (1,980,000 \ J)/(2,700 \ s)$

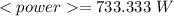
$< power > = 733.333 \ W$

or

$< power > = 0.733 \ kW$