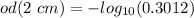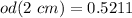Question

I need both parts please (a) Given a material with an attenuation coefficient (a) of 0.6/cm, what is the intensity of a beam (with an incident intensity, lo) after it has traveled through 1 cm of the material? After it has traveled through 2 cm of the material? (b) What is the optical density of a 1 cm thick piece of such a material? Of a 2 cm thick piece of such a material?

Answer 1

a.

• After it has traveled through 1 cm :
  `I(1 \ cm) = 0.5488 I_0`

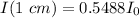
• After it has traveled through 2 cm :
  `I(2 \ cm) = 0.3012 I_0`

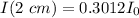
b.

• After it has traveled through 1 cm :
  `od( 1\ cm) =  0.2606`

• After it has traveled through 2 cm :
  `od( 2\ cm) =  0.5211`

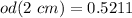
Step-by-step explanation:

a.

For this problem, we can use the Beer-Lambert law. For constant attenuation coefficient
`\mu` the formula is:

`I(x) = I_0 e^(-\mu x)`

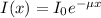
where I is the intensity of the beam,
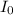`I_0` is the incident intensity and x is the length of the material traveled.

For our problem, after travelling 1 cm:

`I(1 \ cm) = I_0 e^{- 0.6 (1)/(cm) \ 1 cm}`

`I(1 \ cm) = I_0 e^(- 0.6)`

`I(1 \ cm) = I_0 e^(- 0.6)`

`I(1 \ cm) = 0.5488 \ I_0`

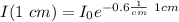
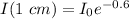
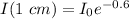
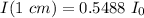
After travelling 2 cm:

`I(2 \ cm) = I_0 e^{- 0.6 (1)/(cm) \ 2 cm}`

`I(2 \ cm) = I_0 e^(- 1.2)`

`I(2 \ cm) = I_0 e^(- 1.2)`

`I(2 \ cm) = 0.3012 \ I_0`

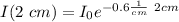
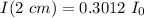
b

The optical density od is given by:

`od(x) = - log_(10) ( (I(x))/(I_0) )`.

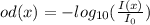So, after travelling 1 cm:

`od( 1\ cm) = - log_(10) ( (0.5488 \ I_0)/(I_0) )`

`od( 1\ cm) = - log_(10) ( 0.5488 )`

`od( 1\ cm) = - (  - 0.2606)`

`od( 1\ cm) =  0.2606`

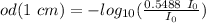
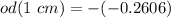
After travelling 2 cm:

`od( 2\ cm) = - log_(10) ( (0.3012 \ I_0)/(I_0) )`

`od( 2\ cm) = - log_(10) ( 0.3012 )`

`od( 2\ cm) = - (  - 0.5211)`

`od( 2\ cm) =  0.5211`