Answer:
The packet should be released approximately 2169 meters before the target, to hit it
Explanation:
Trajectory of the packet:
x = 98*t
y = -4.9*
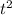 + 3500
+ 3500
t ≥ 0
If we do y = 0 we can determine t for when the packet hit ground (the time between drop and hit)
y = -4.9*
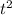 + 3500
+ 3500
0 = -4.9*
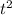 + 3500
+ 3500
t =

Then using the equation of x, we can calculate how far in horizontal direction the packet must be drop to hit the target in the calculated t .
x = 98*t
x= 98 *

x= 2169
The packet should be released approximately 2169 meters before the target, to hit it