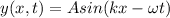Answer:
 and the wave is traveling in the positive x-direction, since we have a wave function like this,
and the wave is traveling in the positive x-direction, since we have a wave function like this,
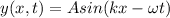
Step-by-step explanation:
A transverse harmonic wave traveling in the x axis is defined by:
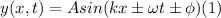
Where A is the amplitude, k the wave number.
 the angular frequency,
the angular frequency,
 the phase constant and the
the phase constant and the
 of the term
of the term
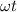 gives us the direction of propagation
gives us the direction of propagation
Recall that
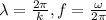 and
and
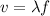
Where
 is the wavelength,
is the wavelength,
 the frequency and
the frequency and
 the phase velocity.
the phase velocity.
We have:
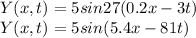
So, you can relate our wave function with the general wave function(1):
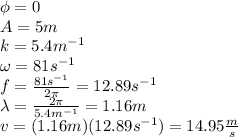
The wave is traveling in the positive x-direction, since we have a wave function like this,