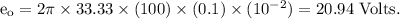Answer:
(a):
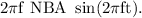 .
.
(b): 20.94 Volts.
Step-by-step explanation:
Given:
- Area of the coil = A.
- Number of turns of the coil = N.
- Magnetic field in which the coil is placed = B.
- The frequency with which the coil is rotating = f.
(a):
The magnetic flux linked with a coil is defined as
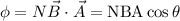
where,
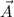 is the area vector of the coil, directed along the normal to the plane of the coil.
is the area vector of the coil, directed along the normal to the plane of the coil.
 = angle between the magnetic field and the area vector of the coil.
= angle between the magnetic field and the area vector of the coil.
Assuming that the magnetic field is along the normal to the plane of the coil, initially.
Therefore, at any later time t, the angle which the magnetic field makes with the normal to the plane of the coil is is given by
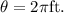
Therefore, the magnetic flux linked with the coil at any time t is given by
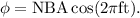
According to the Faraday's law of electromagnetic induction, the emf induced in the coil is given by
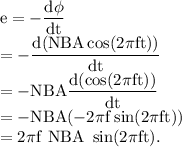
(b):
The amplitude of the alternating voltage is the maximum value of the induced emf in the coil, the induced emf in the coil is maximum when
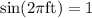 .
.
Therefore, the amplitude of the alternating voltage is given by
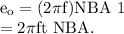
Given values are:
- N = 100 turns.
- A =
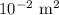 .
. - B = 0.1 T.
- f = 2000 rev/min =
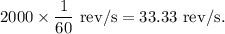
Putting all these values,