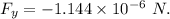Answer:
The y-component of the electric force on this charge is
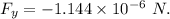
Step-by-step explanation:
Given:
- Electric field in the region,
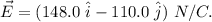
- Charge placed into the region,
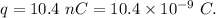
where,
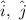 are the unit vectors along the positive x and y axes respectively.
are the unit vectors along the positive x and y axes respectively.
The electric field at a point is defined as the electrostatic force experienced per unit positive test charge, placed at that point, such that,
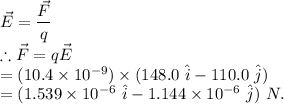
Thus, the y-component of the electric force on this charge is