Question

Two trains face each other on adjacent tracks. They are initially at rest, and their front ends are 50 m apart. The train on the left accelerates rightward at 1.15 m/s2. The train on the right accelerates leftward at 1.15 m/s2. (a) How far does the train on the left travel before the front ends of the trains pass? 25 m (b) If the trains are each 150 m in length, how long after the start are they completely past one another, assuming their accelerations are constant?

Answer 1

The relative acceleration between two trains accelerating towards each other is combined to find the distance and time taken for the trains to pass and clear each other, using the equations of motion.

Step-by-step explanation:

If the train on the left accelerates rightward at 1.15 m/s2 and the train on the right accelerates leftward at the same rate, the relative acceleration between them is 2.3 m/s2 since they are accelerating in opposite directions. When considering the distance between the front ends of the trains, which is 50 m, we can utilize the equation of motion s = ut + (1/2)at2 where 's' is the displacement, 'u' is the initial velocity, 'a' is acceleration, and 't' is time. As both trains start from rest (u = 0), the equation simplifies to s = (1/2)at2.

For part (b), after the front ends pass, we want the back ends to clear each other too. This happens when both trains have collectively covered a distance equal to the sum of their lengths plus the initial distance between their front ends, which is 150 m + 150 m + 50 m = 350 m. We again use the relative acceleration and the equation of motion to solve for the time. The distance each train travels is half of the total distance, or 175 m.

Answer 2

(a) d' = 22.73 m

(b) t = 13.187 s

Solution:

As per the question:

Initial speed of both the trains, u = 0 m/s

The distance between the front ends of the train, d = 50 m

Acceleration of the train on the left,
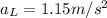`a_(L) = 1.15 m/s^(2)` towards right

Acceleration of the train on the right,
`a_(R) = 1.15 m/s^(2)` towards left

Relative acceleration of the train ,
`a_(r) = 1.15 - (- 1.15) = 2.30 m/s^(2)`

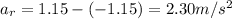
Now,

(a) Using the eqn (2) of motion, for the train on the left:

`d = ut + (1)/(2)a_(r)t^(2)`

`50 = 0.t + (1)/(2)* 2.30t^(2)`

`t = \sqrt{(100)/(2.30)} = 6.593 s`

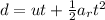
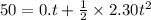
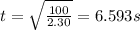
Now, the distance covered by the train on the left before passing the front end:

`d' = ut + (1)/(2)a_(L)t^(2)`

`d' = 0.t + (1)/(2)* 1.15* (6.593)^(2)`

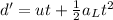
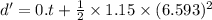
d' = 43.073 m

d' = 43.073 - 25 = 22.73 m

(b) Now,

Acceleration is constant at
`a_(r) = 2.3 m/s^(2)`

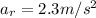
Length of the trains, l = 150 m

Total distance, D = l + d = 150 + 50 = 200 m

Now, from eqn (2) of motion again:

200 = 0.t +
`(1)/(2)* 2.3t^(2)`

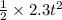
t = 13.187 s