Question

Given vectors D (3.00 m, 315 degrees wrt x-axis) and E (4.50 m, 53.0 degrees wrt x-axis), find the resultant R= D + E. (a) Write R in vector form. (b) Write R showing the magnitude and direction in degrees.

Answer 1

(a)
`\vec{R}= 4.83\ m\ \hat{i}+1.47\ m\ \hat{j}`

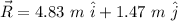
(b) (5.05 m, 16.93 degrees wrt x-axis)

Step-by-step explanation:

Given:

• 
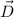  `\vec{D}` = (3.00 m, 315 degrees wrt x-axis)
• 
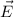  `\vec{E}` = (4.50 m, 53.0 degrees wrt x-axis)

Let us first fond out vector D and E in their rectangular form.

`\vec{D} = (3\cos 315^\circ\ \hat{i}+3\sin 315^\circ\ \hat{j})\ m\\\Rightarrow \vec{D} = (2.12\ \hat{i}-2.12\ \hat{j})\ m\\`

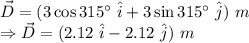
Similarly,

`\vec{E} = (4.5\cos 53^\circ\ \hat{i}+4.5\sin 53^\circ\ \hat{j})\ m\\\Rightarrow \vec{D} = (2.71\ \hat{i}+3.59\ \hat{j})\ m\\\because \vec{R}=\vec{D}+\vec{E}\\\therefore \vec{R} = (2.12\ \hat{i}-2.12\ \hat{j})\ m+(2.71\ \hat{i}+3.59\ \hat{j})\ m\\\Rightarrow \vec{R} = (4.83\ \hat{i}+1.47\ \hat{j})\ m`

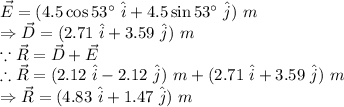
Part (a):

We can write the resultant vector R as below:

`\vec{R} = (4.83\ \hat{i}+1.47\ \hat{j})\ m`

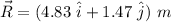
Part (b):

`Magnitude\ of\ resultant = √(4.83^2+1.47^2)\ m = 5.05\ m\\\textrm{Direction in angle with the x-axis} = \theta = \tan^(-1)((1.47)/(4.83))= 16.93^\circ`

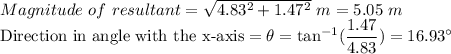
Since both the components of the resultant lie on the positive x and y axes. So, the resultant makes an acute angle with the positive x-axis.

So, R = (5.05 m, 16.93 degrees wrt x-axis)