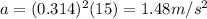Question

A Ferris wheel with a 15-m radius makes three complete revolutions in one minute about its horizontal axis. What is the magnitude and direction of a passengers acceleration at the lowest point during the ride?

Answer 1

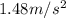`1.48 m/s^2`, upward

Step-by-step explanation:

The passenger on the wheel experiences a centripetal acceleration, which is the one that keeps him in a circular motion.

The direction of this acceleration is always towards the centre of the circular trajectory: so when the passenger is at the lowest point of the ride, the acceleration is upward.

Concerning the magnitude, it is given by

`a=\omega^2 r`

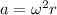
where

`\omega` is the angular velocity

r = 15 m is the radius

We need to find the angular velocity; we know that the wheel completes 3 revolutions in one minute. Each revolution corresponds to an angle of
`2\pi` rad, so the total angular displacement is

`\theta = 3 \cdot 2\pi = 6\pi` rad

And the time is

`t = 1 min = 60 s`

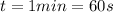
So the angular velocity is

`\omega = (6\pi)/(60 s)=0.314 rad/s`

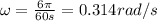
And substituting into the equation of the acceleration,

`a=(0.314)^2(15)=1.48 m/s^2`