Question

A ball is thrown into the air by a baby alien on a planet in the system of Alpha Centauri with a velocity of 35 ft/s. Its height in feet after t seconds is given by y=35t−26t2. A. Find the average velocity for the time period beginning when t=3 and lasting .01 sec : .005 sec : .002 sec : .001 sec : NOTE: For the above answers, you may have to enter 6 or 7 digits if you are using a calculator. B. Estimate the instantaneous velocity when t=3.

Answer 1

Part A:

(a): -121.26 ft/s.

(b): -121.13 ft/s.

(c): -121.052 ft/s.

(d): -121.026 ft/s.

Part B:

-121.00 ft/s.

Step-by-step explanation:

Given that the height of the balloon after t seconds is

`\rm y(t) = 35 t-26t^2.`

The average velocity of an object is defined as the total distance traveled by the object divided by the time taken in covering that distance.

`\rm v_(av) = (y_2-y_1)/(t_2-t_1)`

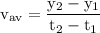
where,

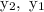`\rm y_2,\ y_1` are the positions of the object at time
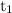`\rm t_1` and
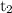`\rm t_2` respectively.

Part A:

• For the average velocity for the time period beginning when t=3 and lasting .01 sec.

For this case,

`\rm t_1 = 3\ sec.\\t_2 = 3+0.01\ sec = 3.01\ sec.\\\\Therefore, \\\\y_1 = 35\cdot 3-26\cdot 3^2=-129\ ft.\\y_2 = 35\cdot 3.01-26\cdot 3.01^2=-130.2126\ ft.\\\\\Rightarrow v_(av)=(-130.2126-(-129))/(3.01-3)=-121.26\ ft/s.`

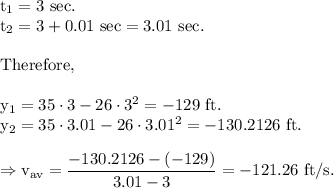
• For the average velocity for the time period beginning when t=3 and lasting .005 sec.

For this case,

`\rm t_1 = 3\ sec.\\t_2 = 3+0.005\ sec = 3.005\ sec.\\\\Therefore, \\\\y_1 = 35\cdot 3-26\cdot 3^2=-129\ ft.\\y_2 = 35\cdot 3.005-26\cdot 3.005^2=-129.60565\ ft.\\\\\Rightarrow v_(av)=(-129.60565-(-129))/(3.005-3)=-121.13\ ft/s.`

• For the average velocity for the time period beginning when t=3 and lasting .002 sec.

For this case,

`\rm t_1 = 3\ sec.\\t_2 = 3+0.002\ sec = 3.002\ sec.\\\\Therefore, \\\\y_1 = 35\cdot 3-26\cdot 3^2=-129\ ft.\\y_2 = 35\cdot 3.002-26\cdot 3.002^2=-129.2421\ ft.\\\\\Rightarrow v_(av)=(-129.2421-(-129))/(3.002-3)=-121.052\ ft/s.`

• For the average velocity for the time period beginning when t=3 and lasting .001 sec.

For this case,

`\rm t_1 = 3\ sec.\\t_2 = 3+0.001\ sec = 3.001\ sec.\\\\Therefore, \\\\y_1 = 35\cdot 3-26\cdot 3^2=-129\ ft.\\y_2 = 35\cdot 3.001-26\cdot 3.001^2=-129.121\ ft.\\\\\Rightarrow v_(av)=(-129.121-(-129))/(3.001-3)=-121.026\ ft/s.`

Part B:

The instantaneous velocity of the balloon at the given time is defined as the rate of change of its position at that time.

`\rm v(t) = (dy)/(dt)\\=(d)/(dt)\left ( 35 t-26t^2\right )\\\\=35-26* 2t.\\\\At\ t=3,\\\\v(t)=35-26* 2* 3=-121.00\ ft/s.`

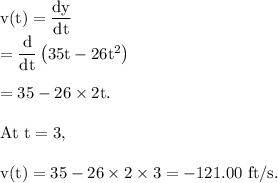
Note: The negative sign with all the velocities indicates that the direction of these velocities are downwards.