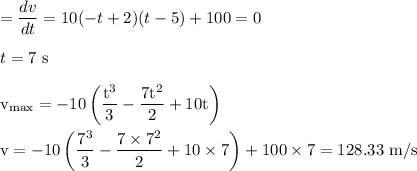Answer:
a)36.33 m
b)346.7 m/s
c)7 s
d)128.33 m/s
Step-by-step explanation:
Given:
Variation of acceleration with time,
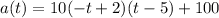
Now using the calculus we have
/(dt)=-10\left ((t^3)/(3)-(7t^2)/(2)+10t \right )](https://img.qammunity.org/2020/formulas/physics/college/z3t53rb955oeizcigf52lhod9b5zbnko94.png)
Again using calculus we have
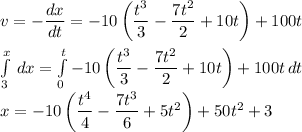
a) At t =2 we have displacement
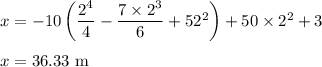
b) Now Let v be the velocity at t=4 s then

c Let t be the time at which the Maximum displacement occurs
Then to Find the time maximum value we will equate the derivative of x with time to 0
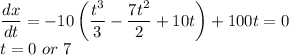
At t=0 we have minimum value of the displacement as the body starts at this time. So the particle will have maximum displacement at t=7 s.
d) In order to find the maximum value of velocity we will equate the derivative of v with respect to time equal to 0