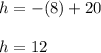Question

Extra points!! A candle is 17 in tall after burning for 3 hours. After 5

hours, it is 15 in, tall. Write a linear equation to
model the relationship between heighth of the candle and time t. Predict how tall the candle will be after burning 8 hours? Please show your steps and explain your work:))
Everything helps!! Thank you so much in advance!!

Answer 1

1)
`h=-t+20`

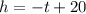
2) 12 inches tall.

Explanation:

1) The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

In this case:

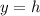`y=h` (The height of the candle in inches)

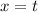`x=t` (The time in hours)

Then, we can rewrite it:

`h=mt+b`

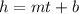
Based on the information provided in the exercise, the line passes through these points:

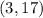`(3,17)` and
`(5,15)`

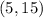
Then, we can find the slope of the line with the formula
`m=(y_2-y_1)/(x_2-x_1)`:

`m=(15-17)/(5-3)=-1`

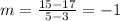
Now we need to substitute the slope and one of the points into
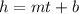`h=mt+b` and then solve for "b":

`17=(-1)(3)+b\\\\b=17+3\\\\b=20`

Substituting values, we get that the a linear equation that models the relationship between the heigth of the candle and the time, is:

`h=-t+20`

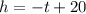
2) We must substitute
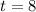`t=8` into the linear equation
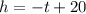`h=-t+20` in order to find the height of the candle after burning 8 hours:

`h=-(8)+20\\\\h=12`