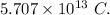Answer:
Step-by-step explanation:
Given,
- Mass of the earth =
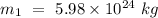
- Mass of the moon =
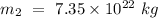
- universal gravitational constant = G =
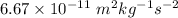
Let Q be charges on the both earth and the moon, and 'r' be the distance between the earth and the moon.
Gravitational force between the earth and the moon is attractive while electrical force between the earth and the moon is repulsive due to identical charges. Hence both are opposite in the sing but are equal in magnitude

Hence, the charges on both the earth and the moon are the same as of