Question

An electron is released from rest at a distance of 6.00 cm from a proton. If the proton is held in place, how fast will the electron be moving when it is 3.00 cm from the proton?

Answer 1

91.87 m/s

Step-by-step explanation:

Given:

• x = initial distance of the electron from the proton = 6 cm = 0.06 m

• y = initial distance of the electron from the proton = 3 cm = 0.03 m
• u = initial velocity of the electron = 0 m/s

Assume:

• m = mass of an electron =
  `9.1* 10^(-31)\ kg`
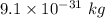
• v = final velocity of the electron
• e = magnitude of charge on an electron =
  `1.6* 10^(-19)\ C`

• p = magnitude of charge on a proton =
  `1.6* 10^(-19)\ C`

We know that only only electric field due to proton causes to move from a distance of 6 cm from proton to 3 cm distance from it. This means the electric force force does work on the electron to move it from one initial position to the final position which is equal to the change in potential energy of the electron due to proton.

Now, according to the work-energy theorem, the total work done by the electric force on the electron due to proton is equal to the kinetic energy change in it.

`\therefore \textrm{Kinetic energy change}= \textrm{Change in potential energy}\\\Rightarrow (1)/(2)m(v^2-u^2)= (kpe)/(y)-(kpe)/(x)\\\Rightarrow (1)/(2)m(v^2-(0)^2)= (kpe)/(0.03)-(kpe)/(0.06)\\\Rightarrow (1)/(2)mv^2= (100kpe)/(3)-(100kpe)/(6)\\\Rightarrow (1)/(2)mv^2= (100kpe)/(6)\\`

`\Rightarrow v^2= (100kpe* 2)/(6m)\\\Rightarrow v^2= (100kpe)/(3m)\\\Rightarrow v^2= (100* 9* 10^9* 1.6* 10^(-19)* 1.6* 10^(-19))/(3* 9.1* 10^(-31))\\\Rightarrow v^2=8.44* 10^3\\\Rightarrow v=91.87\ m/s\\`

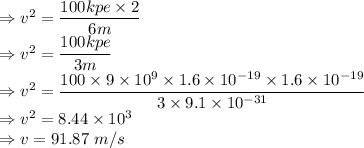
Hence, when the electron is at a distance of c cm from the proton, it moves with a velocity of 91.87 m/s.