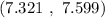Answer:
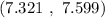
Explanation:
Given : Sample size : n= 400 () large sample
Significance level :
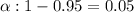
By using Standard normal table , Critical value :
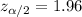
Sample mean :
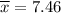
Standard deviation:
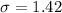
The confidence interval for population means is given by :-
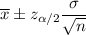
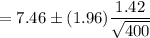
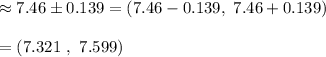
Hence, the 95 percent confidence interval for the mean percentage share of billing volume from network television for the population of all U.S. advertising agencies =