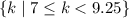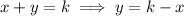
Substitute this into the parabolic equation,

We're told the line
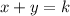 intersects
intersects
 twice, which means the quadratic above has two distinct real solutions. Its discriminant must then be positive, so we know
twice, which means the quadratic above has two distinct real solutions. Its discriminant must then be positive, so we know
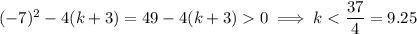
We can tell from the quadratic equation that
 has its vertex at the point (3, 6). Also, note that
has its vertex at the point (3, 6). Also, note that
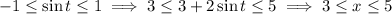
and
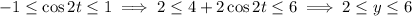
so the furthest to the right that
 extends is the point (5, 2). The line
extends is the point (5, 2). The line
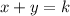 passes through this point for
passes through this point for
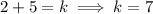 . For any value of
. For any value of
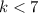 , the line
, the line
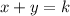 passes through
passes through
 either only once, or not at all.
either only once, or not at all.
So
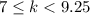 ; in set notation,
; in set notation,