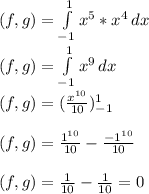Question

What does it mean for two functions to be "orthogonal"? Then, give a specific example of two orthogonal functions.

Answer 1

Step-by-step explanation:

Two functions of a certain space are orthogonal if its inner product is null. Therefore that two particular functions are orthogonal depends on how the inner product has been defined. The most common definition is as follows:

Two functions f and g, continuous and defined in the interval [a, b] are orthogonal in said interval if:

`(f,g)=\int\limits^b_a {f(x})g(x) \, dx =0`

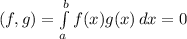
The functions
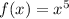`f(x)=x^5` and
`g(x)=x^4` are orthogonal in [-1, 1].

`(f,g)=\int\limits^1_(-1) {x^5*x^4} \, dx \\(f,g)=\int\limits^1_(-1) {x^(9)} \, dx\\(f,g)=((x^(10))/(10))^1_(-1)\\\\(f,g)=(1^(10))/(10)-(-1^(10))/(10)\\\\(f,g)=(1)/(10)-(1)/(10)=0`