Question

Suppose an event is measured to be at a = (0,-2, 3, 5) in one reference frame. Find the components of this event in another reference frame that is moving with a speed of 0.85 relative to the original frame, in the positive x-direction

Answer 1

The coordinates of the same event in this moving frame are a' = (3.226, -3.7966, 3, 5).

Step-by-step explanation:

Given:

• The event in the first reference frame is a = (0,-2, 3, 5).

• The speed of the second reference frame with the respect to the first reference frame = 0.85.

The coordinates of the event are given as (t, x, y, z)

Therefore, for the first frame, the event a has coordinates:

t = 0

x = -2

y = 3

z = 5.

The coordinates of the same event in the moving frame as given by the Lorentz transformation as

`\rm t'=\gamma(t-(vx)/(c^2))\\ x'=\gamma (x-vt).\\y'=y.\\z'=z.`

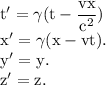
where,

`\rm \gamma = \frac{1}{\sqrt{1-(v^2)/(c^2)}}`

In natural system of units, c = 1.

Therefore,

`\rm \gamma = \frac 1{√(1-v^2)}=(1)/(√(1-0.85^2))=1.898.`

`\rm t'=1.898(0-0.85*(-2))=3.226\\ x'=1.898(-2-0* 0.85)=-3.7966.\\y'=3.\\z'=5.`

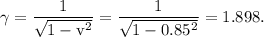
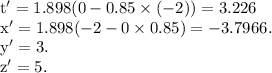
The coordinates of the same event in this moving frame are a' = (3.226, -3.79, 3, 5).

Answer 2

(2.3529, -3.7966, 3,5)

Step-by-step explanation:

We can do this simply by taking the Lorentz transformations:

Taking the coordinates

`t \\x \\y\\\z\\`

in one reference frame, and taking the second reference frame moving at speed v in the x-direction of the original frame, the Lorentz transformations are:

`ct' = \frac{1}{\sqrt{ 1 - (v^2)/(c^2)}}  ( ct - (v)/(c) x )`

`x' = \frac{1}{\sqrt{ 1 - (v^2)/(c^2)}}  ( x' - (v)/(c) ct )`

`y' = y`

`z' = z`

For our problem

`t= 0\\x=-2\\y=3\\z=5\\v=0.85 c`

So, the transformation will give

`ct' = (1)/( √( 1 - 0.85^2 ))  ( 0 - 0.85 * (-2) )`

`ct' =  (1.7)/(0.5267)`

`ct' =  2.3529`

`x' = (1)/(√( 1 - 0.85^2)) ( (-2) - 0.85 * 0 )`

`x' =  (- 2)/(0.5267)`

`x' =  -3.7966`

`y' = 3`

`z' = 5`