Answer:
The following proof makes use of logic equivalences.
Explanation:
We have to show that
 is equivalent to say that
is equivalent to say that
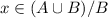 . In fact, if
. In fact, if
 , by definition this is equivalent to say that
, by definition this is equivalent to say that
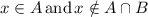 , this is equivalent to say that
, this is equivalent to say that
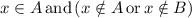 , this is equivalent to
, this is equivalent to
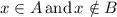 , and this is equivalent to say that
, and this is equivalent to say that
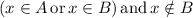 , and this is equivalent to say that
, and this is equivalent to say that
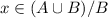 .
.
The Following image can be useful.