Question

Definition: A fraction a/b is reduced if a and b are relatively prime.

Prove: Every rational number is represented by one and only one reduced fraction with a positive denominator.

Answer 1

it is true

Explanation:

We can demonstrate this by contradiction.

First choosing a random rational and assuming that exist two ways to represent this rational. Call that rational x, a, b and a', b ' the couples of relatively prime to express x.

Then we have

`x=x\\(a)/(b)=(a')/(b')`

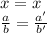
Isolating a:

`a=(a'b)/(b')`

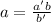
a is an integer and a' is a relatively prime with b', for this reason b has to be a factor of b'. Suppose this factorization b'=nb, replacing it:

`a=(a'nb')/(b')=a'n`

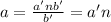
But now we have that n is a factor of a and is a factor of b, it means that a and b are not relatively prime, that is a contradiction with our premises. The sentence is true.

And referring to the positive denominator. If we want to express a positive rational the denominator and numerator will be both positive and if is a negative one we choose a positive denominator and a negative numerator.