Question

Find the optimal solution for the following problem. (Round your answers to 3 decimal places.)

Maximize C = 9x + 7y
subject to 8x + 10y ≤ 17
11x + 12y ≤ 25
and x ≥ 0, y ≥ 0.
1. what is the optimal value of x?

2. What is the optimal value of y?

3. What is the maximum value of the objective function?

Answer 1

x=2.125

y=0

C=19.125

Explanation:

To solve this problem we can use a graphical method, we start first noticing the restrictions
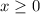`x\geq 0` and
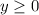`y\geq 0`, which restricts the solution to be in the positive quadrant. Then we plot the first restriction
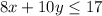`8x+10y\leq 17` shown in purple, then we can plot the second one
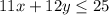`11x+12y\leq 25` shown in the second plot in green.

The intersection of all three restrictions is plotted in white on the third plot. The intersection points are also marked.

So restrictions intersect on (0,0), (0,1.7) and (2.215,0). Replacing these coordinates on the objective function we get C=0, C=11.9, and C=19.125 respectively. So The function is maximized at (2.215,0) with C=19.125.