Answer:
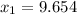 and
and

Explanation:
Given :
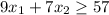
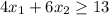
To Find : Find the values of
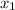 and
and
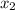 where the following two constraints intersect.
where the following two constraints intersect.
Solution:
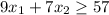
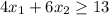
Plot these constraints on the graph
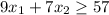 --- Red
--- Red
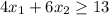 --- Blue
--- Blue
The intersection point will provide the solution
So, Intersection point = (9.654,-4.269)
So,
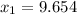 and
and

Refer the attached figure .