Question

Develop an explicit formula in terms of n for the nth term of the following sequence:

0,4,18,48,100,180,......

show that it "works" for the sixth term and use it to find the seventh term.

Answer 1

`a_(n)=(n-1)n^(2)`

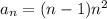
for the seventh term:
`a_(n)=(7-1)7^(2)= (6)(49)=294`

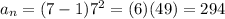
Explanation:

First, we need to observe the sequence, it is crescent, every term is bigger than the one before it. Now, if we put our numbers in a graph (added as an image) we'll notice we obtain an exponential function, this is another detail we'll consider to find our equation, from here it's trial an error.

Our formula is:

`a_(n)=(n-1)n^(2)`

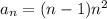
where n is the number of term:

1. 
   `a_(n)=(1-1)1^(2)= (0)(1)=0`
2. 
   `a_(n)=(2-1)2^(2)= (1)(4)=4`
3. 
   `a_(n)=(3-1)3^(2)= (2)(9)=18`
4. 
   `a_(n)=(4-1)4^(2)= (3)(16)=48`
5. 
   `a_(n)=(5-1)5^(2)= (4)(25)=100`
6. 
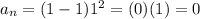
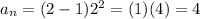
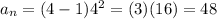
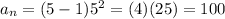
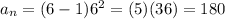   `a_(n)=(6-1)6^(2)= (5)(36)=180` it works!
7. 
   `a_(n)=(7-1)7^(2)= (6)(49)=294`

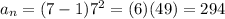
I hope you find this information useful! Good luck!