Answer:
This fact about rational numbers is very simple. Remember
 is a rational number if it is a number of the form
is a rational number if it is a number of the form
 where
where
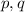 are integers and
are integers and
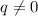 . To prove this result about rational numbers you can consider a rational number
. To prove this result about rational numbers you can consider a rational number
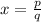 . Then, the square of
. Then, the square of
 is given by
is given by
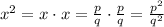
Note that
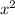 satisfies the definition of a rational numbers.
satisfies the definition of a rational numbers.
Explanation: