Question

A salesperson makes a five percent commission on every sale she makes. Her daily sales in dollars) for the past 16 working days were: 28 49 50 34 33 44 35 25 29 30 35 34 32 40 78 39. a) Find the 5 number summary and P30 b) Find the values of the standard deviation, range, and interquartile range (IQR). c) Are there any outliers? Explain!.

Answer 1

Explanation:

First we arrange these data into ascending order (least to greatest)

25, 28, 29, 30, 32, 33, 34, 34, 35, 35, 39, 40, 44, 49, 50,78

a) 5 number summary :

Minimum : 25

`Q_(1)` =
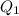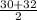`(30+32)/(2)` = 31 [median of first half of the data]

Median :
`(34+35)/(2)` = 34.5

`Q_(3)` =
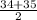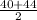`(40+44)/(2)` = 42 [median of first half of the data]

Maximum : 78

For
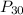`P_(30)` we have to use the formula
`(30n)/(100)`

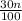
where n = total number of the data

=
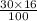`(30* 16)/(100)` = 4.8 ≈ 5

So
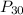`P_(30)` = 5th term of the data = 32

Minimum : 25,
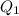`Q_(1)` : 31 Median : 34.5,
`Q_(3)` : 42, Maximum : 78

b) Standard deviation :

Mean of the data :
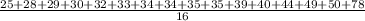`(25+28+29+30+32+33+34+34+35+35+39+40+44+49+50+78)/(16)` = 38.4

Now we will subtract mean and square the result.

25 = -13.4 = 179.56

28 = -10.4 = 108.16

29 = -9.4 = 88.36

30 = -8.4 = 70.56

32 = -6.4 = 40.96

33 = -5.4 = 29.16

34 = -4.4 = 19.36

34 = -4.4 = 19.36

35 = -3.4 = 11.56

35 = - 3.4 = 11.56

39 = 0.6 = 0.36

40 = 1.6 = 2.56

44 = 5.6 = 31.36

49 = 10.6 = 112.36

50 = 50.6 = 134.56

78 = 39.6 = 1568.16

Now take out mean of those results and find the square root.

`(179.56+108.16+88.36+70.56+40.96+29.16+19.36+19.36+11.56+11.56+0.36+2.56+31.36+112.36+134.56+1568.16)/(16)`

=
`(2428)/(16)`

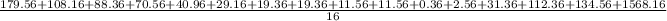
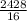
= 151.75

Now square the result
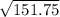`√(151.75)` = 12.3186 ≈ 12.32

Range = Maximum - minimum

= 78 - 25 = 53

Interquartile Range (IQR) =
`Q_(3)- Q_(1)`

= 42 - 31 = 11

c) Outliers : The number of the given data there is a number which is far from the other numbers is called outliers that is 78

Outlier = 78