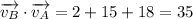Question

Find the projection of the vector A = î - 2ġ + k on the vector B = 4 i - 4ſ + 7k. 15. Given the vectors A = 2 i +3 ſ +6k and B = i +59 +3k. How much of vector B is along vector A?

Answer 1

Part 1) Projection of A along B is 19 units

Part 2) Projection of B' along A' is 35 units.

Explanation:

The projection of any vector A on another vector B is given by the dot product between the two vectors

Given vector A
`\overrightarrow{v_A}=a\widehat{i}+b\widehat{j}+c\widehat{k}`

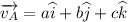
And Vector B

`\overrightarrow{v_B}=l\widehat{i}+m\widehat{j}+n\widehat{k}`

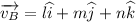
The dot product between them is given by

`\overrightarrow{v_A}\cdot \overrightarrow{v_B}=al+bm+cn`

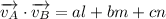
Comparing with the given vectors we have

for vector A

a = 1 ,b = -2, c =1

For vector B

l = 4, m = -4, n = 7

Thus the projection of A along B is

`\overrightarrow{v_A}\cdot \overrightarrow{v_B}=4+8+7=19`

Part b)

For the second case

`\overrightarrow{v_A}=2\widehat{i}+3\widehat{j}+6\widehat{k}`

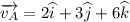
and

`\overrightarrow{v_B}=1\widehat{i}+5\widehat{j}+3\widehat{k}`

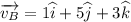
Thus the projection of B along A is

`\overrightarrow{v_B}\cdot \overrightarrow{v_A}=2+15+18=35`